Unit 4: A Wrap Up

In this unit, I learned about a variety of concepts involving rotation. For starters, we learned about tangential and rotational speed. Tangential velocity is the linear speed of something moving along a circular path. Rotational velocity involves the number of rotations an object makes per minute.

The farther from the center, the more an object’s tangential speed increases. This is because there is more mass farther away from the axis of rotation so the object rotates slower- but this has to do with rotational inertia, which I will explain in a moment.

The difference between rotational and tangential speed is that tangential speed increases the farther away from the center the object is, but rotational speed remains the same no matter where the object is. For example, if one person is close to the inside of a merry-go-round, and their friend is riding a horse along the outside, the friend on the outside will have a faster tangential velocity but they will be moving at the same rotational speed. Additionally, if two objects are the same size, they have the same rotational speed. When two objects are different sizes, it is possible for them to have the same rotational speed but different tangential speeds, like the gears shown below:

Although the picture shows circles, imagine that they are gears that interlock. Because they are connected, a point along the edge of the larger gear will cover the same distance as a point on the edge of the smaller gear in an amount of time, meaning that they have the same tangential velocity. However, the smaller gear will be able to rotate once in a shorter amount of time than the larger gear. In fact, these gears share a 1:3 ratio; meaning that the rotational velocity of the smaller gear is faster than that of the larger gear and the smaller one will rotate completely three times in the time it takes the larger gear to rotate once.

Conversely, objects can also have the same rotational velocity and different tangential velocities. Just like on the merry-go-round, this applies to train wheels. They are tapered so that one side of the wheel is wider than the other and two wheels of this shape are connected. Since the sides are connected, they have the same rotational velocity. The wider part of the wheel has a higher tangential velocity and moves faster because it is farther away from the center than the smaller sides of the wheels. This higher tangential velocity causes the wider part of the wheel to curve inward so that the rails are off-center. When one side of the wheel curves, this causes the other side to curve as well and the wheel self corrects. This is why trains sway on the tracks.

Another related concept is that of rotational inertia. This is the property of an object to resist changes in spin (similar to linear inertia which is the property of an object to resist changes in motion). Rotational inertia depends where the mass is located, or the distribution of mass. As I said before, the farther away the mass is from the axis of rotation, the harder it is for an object to spin- aka, the more rotational inertia it has. If the mass is close to the center/axis of rotation, the object has little rotational inertia. When a runner is trying to go faster, they bend their legs. This brings their leg closer to their hip, which is the axis of rotation. Bringing their leg closer brings the mass closer, so the leg/hip system has less rotational inertia and it is easier to rotate/run. The less rotational inertia and object has, the faster its rotational velocity. This allows the runner to go faster. This concept also applies to ice skaters when they do their big finishes with crazy spins.

When an ice skater has her arms spread out and her legs are wide, her mass is distributed farther from her body (axis of rotation) so she has more rotational inertia and she has a low rotational velocity- she is spinning slowly. Then she brings her arms and legs in to her body, drawing the mass in closer to the axis of rotation and decreasing the rotational inertia, allowing her to spin faster. This brings us to the concept of angular, or rotational, momentum. Angular momentum = rotational inertia x rotational velocity. Just like the conservation of linear momentum, there is conservation of angular momentum. When there is a change in an object’s spin, the momentum is the same before and after. So if the ice skater has a high rotational inertia and a low rotational velocity before, and she has a low rotational inertia after, she must also have a high rotational velocity after to equalize the equation and make the momentum before and after her change in spin the same.

Angular Momentum before = Angular Momentum after

Rotational inertia x rotational velocity = rotational inertia x rotational velocity

So by this point, we know a lot about rotation and how it affects an object’s movement. But what causes rotation?

Torque, ladies and gentlemen, causes rotation. A torque is a force exerted over the distance from the axis of rotation. This distance is called a lever arm.

Torque = Force x Lever Arm

There are three ways to increase torque, and therefore increase the rotation of said object:

11)   Increase the force on the object

22)   Increase the lever arm

33)   Increase both the force and the lever arm

The Forces on both sides of the rod being balanced in the picture above are equal. Their lever arms are also equal. This means that they have equivalent forces on both sides of the rod so it is balanced. If one side had a greater torque than the other, this would cause a rotation and the rod would no longer be balanced. Also, if one side had a greater force than the other side but the other side had an equally greater lever arm, the forces would be equal.

Torque = Torque

Force x lever arm = Force x lever arm

(Just like the conservation of momentum)

As a side note, the force must be perpendicularly applied to the lever arm. Torque is measured in units of Newton meters (Nm).

One thing you will notice in the picture above that I have not yet talked about, is the center of gravity. The center of gravity is essentially the same as an object’s center of mass, which is the average position of all the object’s mass. When gravity acts on this exact point, it becomes the object’s center of gravity. This is actually what keeps us from falling over. As long as our center of gravity is above our base of support, there is no lever arm and without a lever arm, no torque can be generated, meaning there is no rotation and we don’t fall over.

In sports, it is easy to be knocked over. But if you change either your center of gravity or your base of support, it is harder to be knocked over. Bending your knees lowers your center of gravity so it is harder to push it out from above the base of support as has been done to the box in the picture above. If you stand with your feet planted at least shoulder width apart (larger than your natural stance) this widens your base of support, which also makes it harder to displace the center of gravity outside the base of support. These two adjustments make it much harder to knock you over.

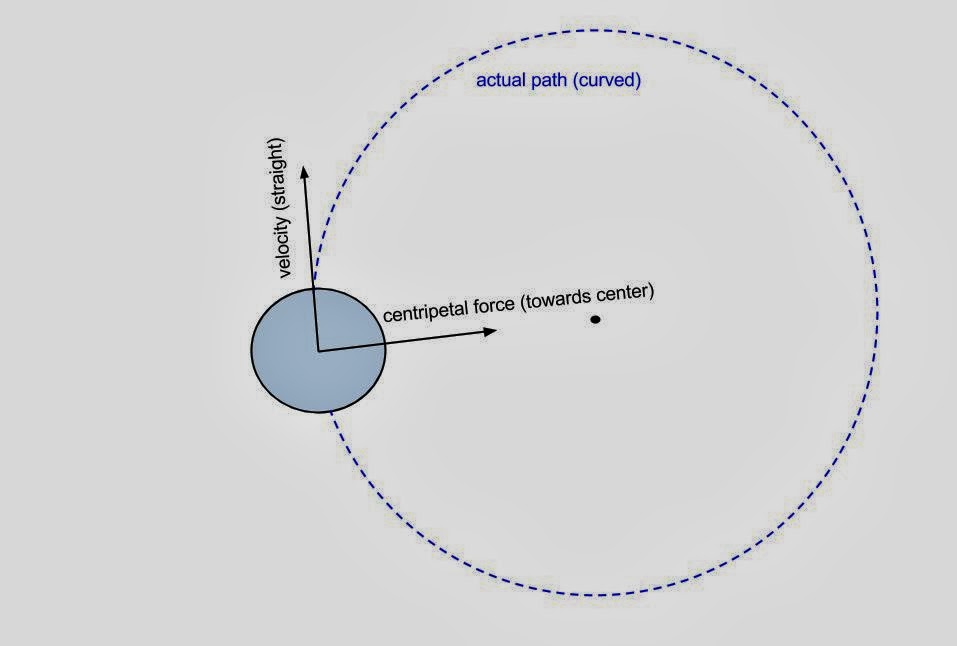
Lastly, we learned about centripetal and centrifugal forces. Centripetal force is a center seeking force. It is the force acting on you, pulling you into a curve. When an object moves, its velocity is always straight. Combined with a centripetal force equal to the velocity, the object can follow a curved path. This is why the moon orbits the Earth (the centripetal force being the pull of Earth’s gravity).

Centrifugal force is a “center fleeing force,” but it is a fictitious force. It is only the feeling of your body responding to the centripetal force pulling you inward. For example, when you are riding in a car, you are moving forward. According to Newton’s 1^st Law of Motion, when an object is in motion, it tends to stay in motion unless acted upon by an outside force. (This is where your inertia comes in! Linear, not rotational). When car you are in turns, your body continues to move forward because 1) velocity is always straight and 2) you have inertia, which causes you to resist changes in motion. Only when the car door pushes into you and forces you to turn with it do you turn. This is the centripetal force acting on you. The feeling of your body not wanting to turn is what we refer to as centrifugal force but it is not actually a force. With a group of classmates, I made a podcast that explains even more clearly the concepts of centripetal and centrifugal forces:

The most difficult thing about what we have studied in this unit has been grasping the visualizations of certain concepts. I am primarily a visual learner so this was a little challenging at times. For example, I have seen ice skaters and we watched videos of ice skaters spinning and getting faster, but I do not know what a train wheel actually looks like aside from the strange diagrams and drawings we looked at in class. Sure, I’ve seen a train wheel before, but not from the angle we were considering. This made the concept of train wheels and their tangential velocities hard to understand at first. I overcame this by just accepting what Mrs. Lawrence was teaching me and applying the concepts to the picture I was provided. Eventually the idea cleared up and I grasped the concept. All it really took was for me to open up to a new perspective.

I think my effort towards homework and quizzes improved noticeably this unit. I studied for nearly all of the small quizzes we took and I spent a lot of time writing out my homework and forming really thorough answers which paid off as it aided in my understanding of the lessons. This boosted my confidence in class when we were discussing some harder problems. Also it developed my communication; I feel pretty good about explaining the information in this unit because I spent so much time explaining it to myself and writing out these explanations in a way that I can go back and read in a few months and still get it. I also think that my group for this podcast collaborated more efficiently and easily than my groups in the past. I am really glad that I will be working with the same group for a little while because I think we work well together and I would say this is one of the more articulate podcasts that I have been a part of making.

My goal for the next unit is to spend more time on my podcast and do something a little more unique. I also am going to have a more positive attitude in class!

I liked this unit a lot, even though I did not immediately “get” everything we talked about. I love sports and just about everything in this unit can be applied to my main sports- I run, so now I understand why bending my legs more will help with sprinting. In playing soccer, I will definitely widen my stance and bend my knees more to keep from being knocked down- which seems to happen to me a lot. Also I have been catching even more physics mistakes in song lyrics since this unit. Yay for physics!

Balancing Act

As we are learning about torque and center of gravity, we are also conducting a lab. Our goal is to find the mass of a  meter stick using only the stick itself and a 100 gram lead weight. We are not allowed to use a scale to find the mass of the meter stick. 

Step 1:

When an object is balanced, the torques on either side of its center of gravity are equal. This means that, collectively, the force and lever arm on either side of the center of gravity are the same. However, one side of the stick could have a long lever arm and little force while the other side could have a lot of force with a short lever arm. As long as the counter-clockwise torque on one side equals the clockwise torque on the other side the object will be balanced because neither rotation overpowers the other so the object will not rotate either way.

When the meter stick is placed on a table with some of it hanging off the edge, the center of gravity (for my group's stick) was at the 50.25 centimeter mark on the stick. This is the point that sits on the very edge of the table where part of the stick can hang off without causing any rotation. 
When a mass is placed on the edge of the meter stick, the center of gravity is shifted to the 29.5 centimeter mark. The distance from the stick's actual center of gravity to the edge of the table, where the new center of gravity is, is now its lever arm, instead of being from the center of gravity to the end of that side of the stick. This means the lever arm is much smaller and that the force on the stick is at the end of this lever arm, not at the end of the stick.

Step 2:

We started with what we already knew about torque and balanced objects. When an object is balanced, the torques on either side of its center of gravity are equal. Therefore, it was essential that:

counter clockwise torque = clockwise torque

Since torque = force x lever arm...

force x lever arm = force x lever arm

Not only were these equations going to be important for us to use, so was the equation for weight, since the whole purpose of the lab was to find the mass of the meter stick. It is:

weight = mass x gravity (w=mg)

We kept in mind the units of all the variables we would be working with.

Weight: Newtons (also in kilogram meters per second squared: kg m/s^2)

Mass: grams and kilograms (100 grams equals 0.1 kilogram)

Gravity: 9.8 meters per second squared (m/s^2)

Force: Newtons

Lever Arm: centimeters (but usually we work in meters for lever arm)

Torque: Newton centimeters (N cm; usually it would be Newton meters)

We chose to use our knowledge of torque for this experiment and our calculations because we knew that force and weight are both in Newtons and are equal. So if we could figure out the torque of one side, we would know both the force on that side (because we could just measure the lever arm and find the force through simple math) and the torque of the other side of the center of gravity because the two torques would be equal). Using this knowledge, we could find the mass through the equation for weight. In order to complete these processes, we took measurements. We found the length of all the lever arms and the point where the center of gravity was. We also found the mass of the weight placed on the meter stick, both in grams and kilograms.

Measurements:

Center of gravity = 50.25 cm mark

Center of gravity with the weight o the meter stick = 29.5 cm mark

Mass of weight = 100 grams (0.1 kilograms)

Lever arm to the left of new center of gravity = 29.5 cm (as shown in picture above)

Lever arm to the right of new center of gravity = 20.75 cm (as shown in picture above)

Step 3:

After we had all of our preliminary measurements taken and our plan of action was established, we began calculating. First, we found the force on the left side of the center of gravity with the weight. Here are our calculations:

w=mg

  = 0.1kg (9.8 m/s^2)

  =0.98 N = Force

Then we found the torque on this portion of the ruler...

torque = force x lever arm

            = (0.98 N)(29.5 cm)

            = 28.91 N cm

Now it was time to find the torque of the other side of the center of gravity...

counter-clockwise torque = clockwise torque

                      [ 28.91 N cm = 28.91 N cm]

               force x lever arm = force x lever arm

              (0.98 N)(29.5 cm) = F (20.75 cm)

                        28.91 N cm = F (20.75 cm)

                                1.39 N = F

Since Force = weight...

1.39 N = weight

weight = mass x gravity

1.39 N = mass (9.8 m/s^2)

0.1418 kg = mass (b/c N also equal kg m/s^2 so when divided, the units cancelled out to kg)
141.8 g = mass
This was our calculated mass (141.8 grams) which we checked on the scale after the experiment concluded. The actual mass of the meter stick was 142.9 grams, so we were very close (only 1.1 grams off).

Torque and Center of Mass

A torque causes rotation. Torque = force x lever arm (the distance of the force from the axis of rotation). The example shown in the video demonstrates torque well as it shows the two sides of the ruler have the same lever arm and their torques are equal so the ruler is balanced on his finger. When I say the torques are "equal," I mean that the counter-clockwise torque on the left side of the ruler and the clockwise torque on the right side of the ruler are equal to each other so they balance each other out. This video, although it does not go into detail, also shows the center of mass. The center of mass is the average position of all the mass of an object. When gravity acts on this point, it is the object's center of gravity. The object's center of gravity is right where the man is supporting the ruler with his finger, which is another reason why it is balanced. 
I think this video is a good resource because it explains torque very clearly and in a lot of detail. The end of the video is actually more advanced than the material we covered in class; we did not learn about the equations he uses. But despite this, I think the rest of the video is clear and helpful. The demonstration shows torque really well, as well as center of gravity even though it does not explicitly go into detail about center of gravity.

Rotational/Angular Momentum

Having already learned about momentum and the conservation of momentum, my class recently learned about angular, or rotational, momentum. To understand rotational momentum, you must first know about rotational inertia. Rotational inertia is the property of an object to resist changes in spin (rotation). The more mass an object has, the greater its rotational inertia is. This also involves the distribution of the mass. When the mass of an object is far away from the axis of rotation, the rotational inertia is greater. When the girl in the video is starting to spin, she keeps her arms extended. This causes her mass to be spread out from her body, where her axis of rotation is, so she spins slowly at first. When she pulls her arms and legs into her body, this changes the distribution of mass so that it is closer to the axis of rotation. She then has a smaller rotational inertia and spins very quickly.

But wait, there's more...

Just as linear momentum is conserved, there is conservation of rotational momentum as well. The total rotational momentum of an object before the change in spin must be equal to the total rotational momentum of the object after the change in spin. Rotational momentum is equal to rotational inertia  x rotational velocity. In the video, we could see how the girl's rotational inertia changed (which I explained) and how it directly affected her velocity. Before the change in her spin, she had a large amount of rotational inertia and a subsequently small rotational velocity. After the change in spin, her rotational inertia was much smaller, and in accordance with conservation of rotational momentum, her rotational velocity increased so that the total momentum was the same before and after the change in spin.

I think this video clearly shows the change. The demonstration would be perfect if there were arrows showing her inertia and such, but I think this is a great rotational momentum resource when coupled with an explanation.